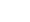What three numbers multiply to get 360?

What three numbers multiply to get 360? In other words, you want to know all the combinations of 3 numbers that can be multiplied to get 360. You want to know what all the question marks in the equation below can be in order for the equation to be true:

? × ? × ? = 360

First, note that all numbers must be 360 or less, which means that there are 360 × 360 × 360 possible solutions. Thus, to get the answer to "What three numbers multiply to get 360?" we looked at 46,656,000 different combinations to see which ones equal 360.

When we looked at all those combinations, we found 180 different combinations of 3 numbers that equal 360 when multiplied together. Here are all 3 number combinations that you can multiply to get 360:

360 × 1 × 1 = 360
180 × 2 × 1 = 360
180 × 1 × 2 = 360
120 × 3 × 1 = 360
120 × 1 × 3 = 360
90 × 4 × 1 = 360
90 × 2 × 2 = 360
90 × 1 × 4 = 360
72 × 5 × 1 = 360
72 × 1 × 5 = 360
60 × 6 × 1 = 360
60 × 3 × 2 = 360
60 × 2 × 3 = 360
60 × 1 × 6 = 360
45 × 8 × 1 = 360
45 × 4 × 2 = 360
45 × 2 × 4 = 360
45 × 1 × 8 = 360
40 × 9 × 1 = 360
40 × 3 × 3 = 360
40 × 1 × 9 = 360
36 × 10 × 1 = 360
36 × 5 × 2 = 360
36 × 2 × 5 = 360
36 × 1 × 10 = 360
30 × 12 × 1 = 360
30 × 6 × 2 = 360
30 × 4 × 3 = 360
30 × 3 × 4 = 360
30 × 2 × 6 = 360
30 × 1 × 12 = 360
24 × 15 × 1 = 360
24 × 5 × 3 = 360
24 × 3 × 5 = 360
24 × 1 × 15 = 360
20 × 18 × 1 = 360
20 × 9 × 2 = 360
20 × 6 × 3 = 360
20 × 3 × 6 = 360
20 × 2 × 9 = 360
20 × 1 × 18 = 360
18 × 20 × 1 = 360
18 × 10 × 2 = 360
18 × 5 × 4 = 360
18 × 4 × 5 = 360
18 × 2 × 10 = 360
18 × 1 × 20 = 360
15 × 24 × 1 = 360
15 × 12 × 2 = 360
15 × 8 × 3 = 360
15 × 6 × 4 = 360
15 × 4 × 6 = 360
15 × 3 × 8 = 360
15 × 2 × 12 = 360
15 × 1 × 24 = 360
12 × 30 × 1 = 360
12 × 15 × 2 = 360
12 × 10 × 3 = 360
12 × 6 × 5 = 360
12 × 5 × 6 = 360
12 × 3 × 10 = 360
12 × 2 × 15 = 360
12 × 1 × 30 = 360
10 × 36 × 1 = 360
10 × 18 × 2 = 360
10 × 12 × 3 = 360
10 × 9 × 4 = 360
10 × 6 × 6 = 360
10 × 4 × 9 = 360
10 × 3 × 12 = 360
10 × 2 × 18 = 360
10 × 1 × 36 = 360
9 × 40 × 1 = 360
9 × 20 × 2 = 360
9 × 10 × 4 = 360
9 × 8 × 5 = 360
9 × 5 × 8 = 360
9 × 4 × 10 = 360
9 × 2 × 20 = 360
9 × 1 × 40 = 360
8 × 45 × 1 = 360
8 × 15 × 3 = 360
8 × 9 × 5 = 360
8 × 5 × 9 = 360
8 × 3 × 15 = 360
8 × 1 × 45 = 360
6 × 60 × 1 = 360
6 × 30 × 2 = 360
6 × 20 × 3 = 360
6 × 15 × 4 = 360
6 × 12 × 5 = 360
6 × 10 × 6 = 360
6 × 6 × 10 = 360
6 × 5 × 12 = 360
6 × 4 × 15 = 360
6 × 3 × 20 = 360
6 × 2 × 30 = 360
6 × 1 × 60 = 360
5 × 72 × 1 = 360
5 × 36 × 2 = 360
5 × 24 × 3 = 360
5 × 18 × 4 = 360
5 × 12 × 6 = 360
5 × 9 × 8 = 360
5 × 8 × 9 = 360
5 × 6 × 12 = 360
5 × 4 × 18 = 360
5 × 3 × 24 = 360
5 × 2 × 36 = 360
5 × 1 × 72 = 360
4 × 90 × 1 = 360
4 × 45 × 2 = 360
4 × 30 × 3 = 360
4 × 18 × 5 = 360
4 × 15 × 6 = 360
4 × 10 × 9 = 360
4 × 9 × 10 = 360
4 × 6 × 15 = 360
4 × 5 × 18 = 360
4 × 3 × 30 = 360
4 × 2 × 45 = 360
4 × 1 × 90 = 360
3 × 120 × 1 = 360
3 × 60 × 2 = 360
3 × 40 × 3 = 360
3 × 30 × 4 = 360
3 × 24 × 5 = 360
3 × 20 × 6 = 360
3 × 15 × 8 = 360
3 × 12 × 10 = 360
3 × 10 × 12 = 360
3 × 8 × 15 = 360
3 × 6 × 20 = 360
3 × 5 × 24 = 360
3 × 4 × 30 = 360
3 × 3 × 40 = 360
3 × 2 × 60 = 360
3 × 1 × 120 = 360
2 × 180 × 1 = 360
2 × 90 × 2 = 360
2 × 60 × 3 = 360
2 × 45 × 4 = 360
2 × 36 × 5 = 360
2 × 30 × 6 = 360
2 × 20 × 9 = 360
2 × 18 × 10 = 360
2 × 15 × 12 = 360
2 × 12 × 15 = 360
2 × 10 × 18 = 360
2 × 9 × 20 = 360
2 × 6 × 30 = 360
2 × 5 × 36 = 360
2 × 4 × 45 = 360
2 × 3 × 60 = 360
2 × 2 × 90 = 360
2 × 1 × 180 = 360
1 × 360 × 1 = 360
1 × 180 × 2 = 360
1 × 120 × 3 = 360
1 × 90 × 4 = 360
1 × 72 × 5 = 360
1 × 60 × 6 = 360
1 × 45 × 8 = 360
1 × 40 × 9 = 360
1 × 36 × 10 = 360
1 × 30 × 12 = 360
1 × 24 × 15 = 360
1 × 20 × 18 = 360
1 × 18 × 20 = 360
1 × 15 × 24 = 360
1 × 12 × 30 = 360
1 × 10 × 36 = 360
1 × 9 × 40 = 360
1 × 8 × 45 = 360
1 × 6 × 60 = 360
1 × 5 × 72 = 360
1 × 4 × 90 = 360
1 × 3 × 120 = 360
1 × 2 × 180 = 360
1 × 1 × 360 = 360

Three Numbers Multiply to Get Calculator
Do you need a different combination of three numbers that when multiplied equal a number other than 360? No problem! Please enter your number here.

What three numbers multiply to get 361?
Here is the next problem on our list that we have explained and answered for your convenience.